Simulating Multi-state Models with R
- Introduction
- An example 6-state model
- Estimation
- Simulation
- Probabilistic sensitivity analysis
- Conclusion
Introduction
Multi-state models are used to model a trajectory through multiple states. Survival models are a special case in which there are two states, alive and dead. Multi-state models are therefore useful in clinical settings because they can be used to predict or simulate disease progression in detail. Putter et al. provide a helpful tutorial.
In this post, we will consider “clock-reset” (i.e., semi-Markov) models rather than “clock-forward” (i.e., Markov) models. In a “clock-reset” model, time refers to time since entering the most recent state, whereas in a “clock-forward” model time refers to time since entering the initial state. When using a “clock-reset” approach, state occupancy probabilities can only be computed in a general fashion via simulation.
The analysis will be restricted to parametric models, which are useful for extrapolating beyond the the time horizon in the existing data. Example probability distributions include the exponential, Weibull, Gompertz, gamma, log-logistic, lognormal, and generalized gamma.
The flexsurv package will be used to estimate the parametric models and the mstate and hesim (admittedly developed by me) packages will be used to simulate the estimated models. We will compare the computational efficiency of different simulation methods.
An example 6-state model
To illustrate, we will follow Wreede et al. and use a 6-state model for leukemia patients following bone marrow transplantation (see figure below). The six states are (1) Transplant (Tx), (2) Recovery (Rec), (3) Adverse Event (AE), (4) AE and Rec, (5) Relapse (Rel), and (6) Death. The following 12 transitions are possible.
- Tx to Rec
- Tx to AE
- Tx to Rel
- Tx to Death
- Rec to AE and Rec
- Rec to Rel
- Rec to Death
- AE to AE and Rec
- AE to Rel
- AE to Death
- AE and Rec to Rel
- AE and Rec to Death
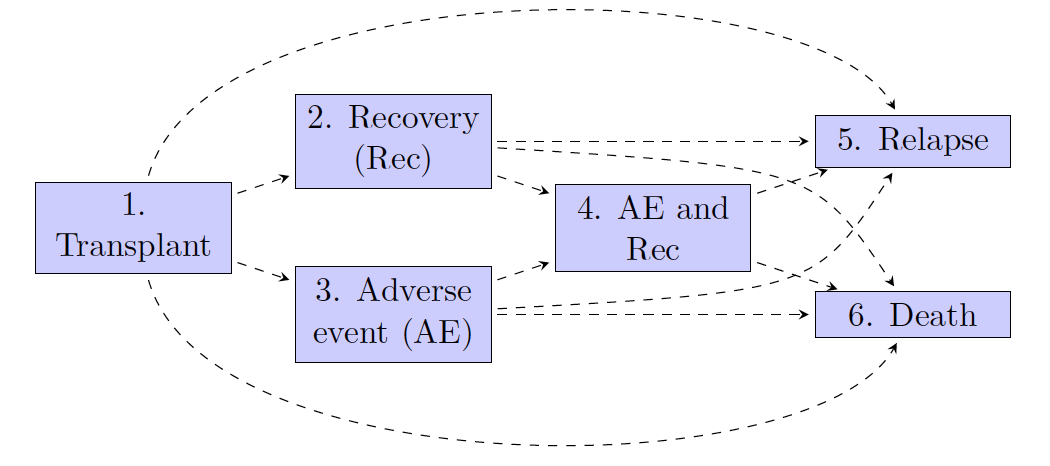
The transitions can be characterized with a 6 x 6 transition matrix, which is a square-matrix where the (i,j) element is a positive integer if a transition from i to j is possible and NA otherwise.
library("mstate")
tmat <- mstate::transMat(x = list(c(2, 3, 5, 6),
c(4, 5, 6),
c(4, 5, 6),
c(5, 6),
c(),
c()),
names = c("Tx", "Rec", "AE", "Rec+AE",
"Rel", "Death"))
print(tmat)
## to
## from Tx Rec AE Rec+AE Rel Death
## Tx NA 1 2 NA 3 4
## Rec NA NA NA 5 6 7
## AE NA NA NA 8 9 10
## Rec+AE NA NA NA NA 11 12
## Rel NA NA NA NA NA NA
## Death NA NA NA NA NA NA
Estimation
Parametric multi-state models can be fit using flexsurv and both non-parametric and semi-parametric models can be fit with mstate. In our analysis, we will fit a parametric model to the ebmt4 dataset from the mstate package. For additional information on model fitting and multi-state data beyond what is provided in this post, I recommend the mstate and flexsurv articles published in the Journal of Statistical Software.
Data
The ebmt4 dataset is in a “wide” format, which is not suitable for multi-state modeling. Luckily, the mstate package contains a helper function, mstate::msprep(), which can convert data in wide format to a suitable “long” format.
library("mstate")
data("ebmt4")
msebmt <- msprep(data = ebmt4, trans = tmat,
time = c(NA, "rec", "ae","recae", "rel", "srv"),
status = c(NA, "rec.s", "ae.s", "recae.s", "rel.s", "srv.s"),
keep = c("match", "proph", "year", "agecl"))
msebmt[msebmt$id == 2, ]
## An object of class 'msdata'
##
## Data:
## id from to trans Tstart Tstop time status match proph
## 8 2 1 2 1 0 12 12 0 no gender mismatch no
## 9 2 1 3 2 0 12 12 1 no gender mismatch no
## 10 2 1 5 3 0 12 12 0 no gender mismatch no
## 11 2 1 6 4 0 12 12 0 no gender mismatch no
## 12 2 3 4 8 12 29 17 1 no gender mismatch no
## 13 2 3 5 9 12 29 17 0 no gender mismatch no
## 14 2 3 6 10 12 29 17 0 no gender mismatch no
## 15 2 4 5 11 29 422 393 1 no gender mismatch no
## 16 2 4 6 12 29 422 393 0 no gender mismatch no
## year agecl
## 8 1995-1998 20-40
## 9 1995-1998 20-40
## 10 1995-1998 20-40
## 11 1995-1998 20-40
## 12 1995-1998 20-40
## 13 1995-1998 20-40
## 14 1995-1998 20-40
## 15 1995-1998 20-40
## 16 1995-1998 20-40
Notice that the data is set up so that there is a time-to-event for each permitted transition from a given state. In the msebmt dataset, this variable is time, which measures the time elapsed (in days) from Tstart to Tstop. The dataset also contains a variable named status, which denotes whether the transition is observed (status = 1) or whether it was censored (status = 0). From a given state, only one transition is observed and all others are censored.
For example, patient 2 began in state 1 (Tx) at time 0. From state 1, there are 4 possible transitions: transition 2 (Tx to AE) was observed at time 12 while transition 1 (Tx to Rec), transition 3 (Tx to Rel), and transition 4 (Tx to Death) were censored. The patient remained in state 3 until time 29, when a transition to state 4 (AE and Rec) occurred and the transitions to states 5 (Rel) and 6 (Death) were censored. Patient 2 subsequently remained in state 4 until entering state 5 (Rel) at time 422, at which time transition 12 (AE and Rec to Death) was censored.
Fitting
Separate hazard functions, $\lambda_{rs}(t|Z)$ are estimated for each possible transition from state $r$ to state $s$ as a function of time $t$ and covariates $Z$. In “clock-reset” models, the hazard function depends on elapsed time since entering state $r$, or simply Tstop - Tstart. The hazard functions can be estimated using a joint model with patient and transition interaction terms or by fitting separate models for each transition.
Here we illustrate by fitting 12 transition-specific Weibull models with a yearly time scale. The shape parameter for each model does not depend on covariates whereas the scale parameter depends on four prognostic factors known at baseline: (1) an indicator for whether the donor is a gender mismatch (match), prophylaxis (yes or no) (proph), (3) the year of the transplant (1985-1989, 1990-1994, 1995-1998) (year), and (4) age at transplant in years (agecl).
library("flexsurv")
n_trans <- max(tmat, na.rm = TRUE)
fits_wei <- vector(mode = "list", length = n_trans)
msebmt$years <- msebmt$time/365.25
for (i in 1:n_trans){
fits_wei[[i]] <- flexsurvreg(Surv(years, status) ~ match + proph + year + agecl ,
data = subset(msebmt, trans == i),
dist = "gompertz")
}
Simulation
We first simulate the model using the maximum likelihood estimates of the regression coefficients; that is, we assume that there is no parameter uncertainty. Outcomes will be simulated for patient 2 with the covariate profile displayed below.
pat_2 <- data.frame(msebmt[msebmt$id == 2,
c("match", "proph", "year", "agecl")][1, ])
head(pat_2)
## match proph year agecl
## 8 no gender mismatch no 1995-1998 20-40
State occupancy probabilities will be computed from baseline to year 10.
yr_grid <- seq(0, 10, .1)
mstate
Multi-state models can be simulated using mstate::mssample(), which simulates state occupancy probabilities from predicted cumulative hazards. flexsurv can be used to predict cumulative hazards for a given patient (i.e., patient 2) given a covariate profile. When predicting the cumulative hazards, it is critical that the time grid (the t argument) is not too coarse. A time step of .01 is used for the time grid, which (after trial and error) was deemed to be sufficiently accurate — simulations with coarser grids differed significantly from simulations based on continuous time using hesim. Finer grids would further increase accuracy but at the cost of slower simulation times.
cumhaz_grid <- seq(0, max(msebmt$years), .01)
cumhaz_pat_2 <- msfit.flexsurvreg(fits_wei, trans = tmat,
t = cumhaz_grid,
newdata = pat_2,
variance = FALSE)
head(cumhaz_pat_2$Haz)
## time Haz trans
## 1 0.00 0.00000000 1
## 2 0.01 0.05802611 1
## 3 0.02 0.11247756 1
## 4 0.03 0.16357455 1
## 5 0.04 0.21152374 1
## 6 0.05 0.25651905 1
tail(cumhaz_pat_2$Haz)
## time Haz trans
## 20431 16.97 0.2366846 12
## 20432 16.98 0.2366849 12
## 20433 16.99 0.2366853 12
## 20434 17.00 0.2366856 12
## 20435 17.01 0.2366859 12
## 20436 17.02 0.2366863 12
The mstate::mssample() function works by sampling survival times from each possible transition from the cumulative hazards. More precisely, the cumulative hazards are used to simulate the (discrete) times at which patients transition between health states using the base R function sample(), which is, in turn, used to count the number of patients in each health state at the times specified by the argument tvec.
The function below uses mstate::mssample() to simulate state occupancy probabilities with a “clock-reset” model at the times specified in yr_grid.
sim_stprobs_mstate_2 <- function(n_pats){
mstate::mssample(Haz = cumhaz_pat_2$Haz,
trans = tmat,
tvec = yr_grid,
clock = "reset",
M = n_pats)
}
hesim
hesim's approach to simulating multi-state models differs from mstate's in a couple of ways. First, if parametric models are estimated, then hesim samples survival times directly from parametric probability distributions (e.g., the Weibull distribution). This increases accuracy (since no discrete time approximation is required) and speed (since it is considerably faster to sample from probability distributions with known functional forms than by sampling from cumulative hazards with sample()). Second, the simulation code is vectorized (i.e., the simulation code is written in C++ by leveraging Rcpp) across heterogeneous patients and treatment strategies. In other words, hesim can be used to quickly simulate multiple covariate profiles and treatment alternatives.
We set up input data for the simulation by creating a dataset of many identical patients each with the covariate profile of patient 2 and a single treatment strategy (i.e., bone marrow transplantation). An example dataset of 1,000 identical patients is displayed. (Note that hesim uses data.table to increase speed.)
library("hesim")
library("data.table")
create_input_data_2 <- function(n_pats){
# Patients
patients <- pat_2[rep(1, n_pats), ]
patients$patient_id <- 1:n_pats
# Treatment strategies
strategies <- data.frame(strategy_id = 1)
# Input data
hesim_dat <- hesim_data(strategies = strategies,
patients = patients)
input_data <- hesim::expand(hesim_dat, by = c("strategies", "patients"))
return(input_data[, ])
}
create_input_data_2(n_pats = 1000)
## strategy_id patient_id match proph year agecl
## 1: 1 1 no gender mismatch no 1995-1998 20-40
## 2: 1 2 no gender mismatch no 1995-1998 20-40
## 3: 1 3 no gender mismatch no 1995-1998 20-40
## 4: 1 4 no gender mismatch no 1995-1998 20-40
## 5: 1 5 no gender mismatch no 1995-1998 20-40
## ---
## 996: 1 996 no gender mismatch no 1995-1998 20-40
## 997: 1 997 no gender mismatch no 1995-1998 20-40
## 998: 1 998 no gender mismatch no 1995-1998 20-40
## 999: 1 999 no gender mismatch no 1995-1998 20-40
## 1000: 1 1000 no gender mismatch no 1995-1998 20-40
hesim combines the input data with the model fit from flexsurvreg() to set up a disease model—specifically, an individual-level continuous time state transition model (CTSTM). Similar to mstate::mssample, the $sim_stateprobs() function simulates state occupancy probabilities by first simulating a trajectory through the multi-state model for each patient and treatment strategy combination and then counting the number of simulated patients (for each treatment strategy) in each state over time.
sim_stprobs_hesim_2 <- function(n_pats, fits, point_estimate = TRUE,
n_samples = 1000){
input_dat_2 <- create_input_data_2(n_pats)
dismod <- create_IndivCtstmTrans(hesim::flexsurvreg_list(fits),
input_dat_2,
trans_mat = tmat,
clock = "reset",
point_estimate = point_estimate,
n = n_samples)
return(dismod$sim_stateprobs(t = yr_grid))
}
Comparison
We simulate state occupancy probabilities using both mstate and hesim and vary the number of simulated patients to examine the impact on precision.
n_pats <- seq(from = 200, to = 1000, by = 200)
stprobs2 <- vector(mode = "list", length = length(n_pats))
for (i in 1:length(n_pats)){
# mstate
mstate_stprobs2 <- sim_stprobs_mstate_2(n_pats[i])
mstate_stprobs2 <- melt(mstate_stprobs2, id.vars = "time",
variable.name = "state_id",
value.name = "prob")
mstate_stprobs2$state_id <- sub("pstate", "", mstate_stprobs2$state_id)
mstate_stprobs2$state_id <- as.numeric(mstate_stprobs2$state_id)
mstate_stprobs2$lab <- "mstate"
# hesim
hesim_stprobs2 <- sim_stprobs_hesim_2(n_pats[i], fits_wei)
hesim_stprobs2$lab <- "hesim"
hesim_stprobs2[, c("sample", "strategy_id") := NULL]
setnames(hesim_stprobs2, "t", "time")
# combine
stprobs2[[i]] <- rbind(mstate_stprobs2, hesim_stprobs2)
stprobs2[[i]]$n_pats <- n_pats[i]
print(i)
}
stprobs2 <- rbindlist(stprobs2)
As shown in the plot below, the differences in state occupancy probabilities generally become smaller as the number of simulated patients increases. Further, (although not shown) the simulation results from mstate become increasingly close to hesim as the time grid becomes finer.
library("ggplot2")
stprobs2[, state_name := factor(state_id, levels = 1:6,
labels = colnames(tmat))]
n_pats_levels <- paste0("Patients = ", unique(stprobs2$n_pats))
stprobs2[, n_pats_name := factor(n_pats, labels = n_pats_levels)]
ggplot(stprobs2, aes(x = time, y = prob, col = lab)) +
geom_line() +
facet_grid(state_name ~ n_pats_name, scales = "free_y") +
xlab("Years") + ylab("Probability in health state") +
scale_x_continuous(breaks = seq(0, max(yr_grid), 2)) +
scale_color_discrete(name = "") + theme_bw() +
theme(legend.position = "bottom")
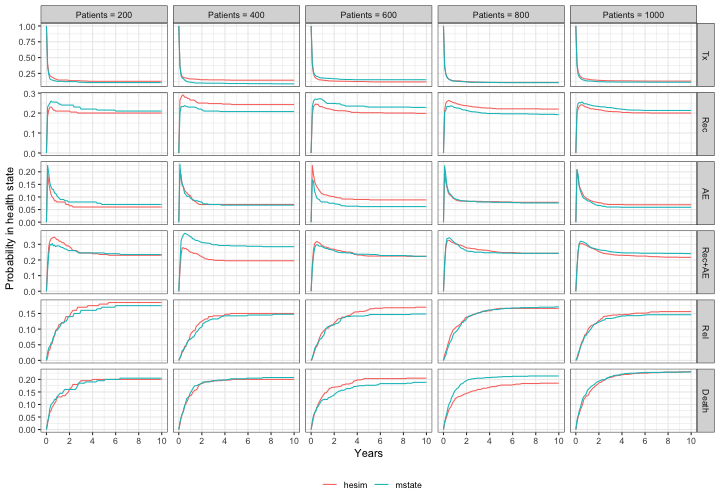
Since 1,000 iterations generate reasonably accurate estimates, we will assess speed by simulating 1,000 patients.
time_mstate <- system.time(sim_stprobs_mstate_2(1000))
time_hesim <- system.time(sim_stprobs_hesim_2(1000, fits_wei))
print(time_mstate)
## user system elapsed
## 19.759 2.674 24.842
print(time_hesim)
## user system elapsed
## 0.036 0.000 0.037
The elapsed times (in seconds) suggest that hesim is 671.41 times faster than mstate when simulating a parametric multi-state model.
Probabilistic sensitivity analysis
The results presented so far have ignored the impact of parameter uncertainty. In contrast, probabilistic sensitivity analysis (PSA) propagates uncertainty in the parameters to the state occupancy probabilities. In our case, the regression coefficients from the multi-state model are drawn from a suitable probability distribution and the multi-state simulation is run for each draw of the coefficients. There are a number of ways to simulate the distribution of the coefficients including bootstrapping, Bayesian modeling, and asymptotic Monte Carlo approximation. We will take the latter approach by sampling the maximum likelihood estimates from an asymptotic multivariate distribution, which is the fastest option.
Although sampling from a multivariate normal distribution is not computationally intensive, repeatedly rerunning the simulation for each draw of the regression coefficients is. In this section, we show how to perform PSA using both mstate and hesim and compare performance.
mstate
PSA can be performed using mstate::mssample() by looping through a distribution of cumulative hazards for a covariate profile and running mstate::mssample() for each iteration of the loop. The most straightforward way to predict a distribution of cumulative hazards is with the CTSTMs from the hesim package. The $cumhazard() function predicts cumulative hazards by transition number, parameter sample, treatment strategy, patient, and time. In our example, we predict cumulative hazards for a single patient (id = 2) and treatment strategy.
# n_samples = # of PSA iterations
predict_cumhaz_dist_2 <- function(n_samples){
input_dat_2 <- create_input_data_2(n_pats = 1)
dismod <- create_IndivCtstmTrans(hesim::flexsurvreg_list(fits_wei),
input_dat_2,
trans_mat = tmat,
clock = "reset",
n = n_samples,
point_estimate = FALSE)
cumhaz_pat2_dist <- dismod$cumhazard(t = cumhaz_grid)
setnames(cumhaz_pat2_dist, c("t", "cumhazard"), c("time", "Haz"))
return(cumhaz_pat2_dist)
}
predict_cumhaz_dist_2(n_samples = 3)
## trans sample strategy_id patient_id time Haz
## 1: 1 1 1 1 0.00 0.00000000
## 2: 1 1 1 1 0.01 0.06755236
## 3: 1 1 1 1 0.02 0.13070470
## 4: 1 1 1 1 0.03 0.18974361
## 5: 1 1 1 1 0.04 0.24493701
## ---
## 61304: 12 3 1 1 16.98 0.23223958
## 61305: 12 3 1 1 16.99 0.23223995
## 61306: 12 3 1 1 17.00 0.23224033
## 61307: 12 3 1 1 17.01 0.23224070
## 61308: 12 3 1 1 17.02 0.23224107
A distribution of simulated state occupancy probabilities for patient 2 can then be simulated by looping over the cumulative hazards for each parameter sample.
psa_stprobs_mstate_2 <- function(n_pats, n_samples){
cumhaz_dist_2 <- predict_cumhaz_dist_2(n_samples)
stprobs_mstate_2 <- vector(mode = "list", length = n_samples)
for (s in 1:n_samples){
cumhaz_s <- cumhaz_dist_2[sample == s]
stprobs_mstate_2[[s]] <- sim_stprobs_mstate_2(n_pats)
stprobs_mstate_2[[s]]$sample <- s
}
stprobs_mstate_2 <- rbindlist(stprobs_mstate_2)
return(stprobs_mstate_2)
}
hesim
With hesim, the entire analysis is inherently Bayesian so PSA is seamless. When creating a CTSTM from a flexsurvreg object, the user must simply set the argument point_estimate = FALSE and choose the number of samples of the parameters to draw. The distribution of the regression coefficients is then drawn by sampling from the multivariate normal distribution. Furthermore, the PSA is vectorized since the loops over the parameter samples are written in C++.
Comparison
In our comparisons, we continue to simulate 1,000 patients. With hesim, we consider both 100 and 1,000 parameter samples; with mstate we restrict the analysis to 100 parameter samples because it becomes increasingly slow as the number of parameter samples increases.
time_mstate <- system.time(psa_stprobs_mstate_2(n_pats = 1000, n_samples = 100))
time_hesim_100 <- system.time(sim_stprobs_hesim_2(n_pats = 1000, fits_wei,
point_estimate = FALSE,
n_samples = 100))
time_hesim_1000 <- system.time(sim_stprobs_hesim_2(n_pats = 1000, fits_wei,
point_estimate = FALSE,
n_samples = 1000))
print(time_mstate)
## user system elapsed
## 1764.489 270.389 2038.770
print(time_hesim_100)
## user system elapsed
## 0.403 0.037 0.440
print(time_hesim_1000)
## user system elapsed
## 4.665 0.422 5.093
hesim is fast, even when performing a PSA. With 1,000 patients, 100 PSA iterations can be simulated in less than a second and 1,000 PSA iterations in approximately 5 seconds. Computational efficiency becomes increasingly important as the computational demands grow: with 1,000 patients and 100 PSA iterations, mstate takes around 34 minutes to run and hesim is 4633.57 times faster.
Conclusion
In this post, we describe some of the R packages that facilitate multi-state modeling. The flexsurv package is particularly useful for estimating parametric models. When “clock-reset” models are fit, state occupancy probabilities can only be predicted for general multi-state models using simulation. Both the hesim and mstate packages provide functionality for running such simulations. However, when parametric models are fit, hesim is considerably faster and this computational advantage grows with the number of required iterations. The speed advantage may be particularly useful when running a PSA, multiple subgroup analyses, and/or simulations using competing survival distributions.